1. 3.1 Product Ruleap Calculus Calculator
2. 3.1 Product Ruleap Calculus Solver
3. 3.1 Product Ruleap Calculus Formulas
4. 3.1 Product Ruleap Calculus 14th Edition

0.3 1.4 1.1 22 2 40.75 PP P P P PP vv v v vtdt vv 1: answer, using trapezoidal sum (c) vt t A t BQ 60 1.866181 or 3.519174 vtQ 60 for At B 106.108754 B Q A vt dt The distance traveled by particle Q during the interval At B is 106.109 (or 106.108) meters. 1: interval 3: 1: definite integral. A mathematical constant is a key number whose value is fixed by an unambiguous definition, often referred to by a symbol (e.g., an alphabet letter), or by mathematicians' names to facilitate using it across multiple mathematical problems.

Show Mobile NoticeShow All NotesHide All Notes

Section 3-4 : Product and Quotient Rule

In the previous section we noted that we had to be careful when differentiating products or quotients. It’s now time to look at products and quotients and see why.

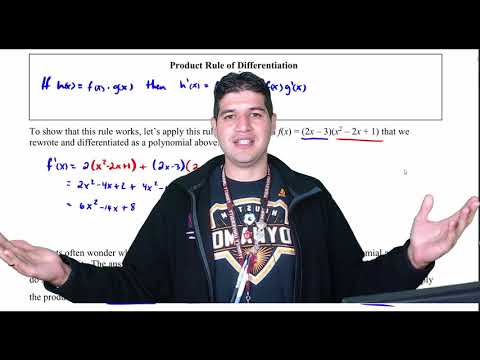
First let’s take a look at why we have to be careful with products and quotients. Suppose that we have the two functions (fleft( x right) = {x^3}) and (gleft( x right) = {x^6}). Let’s start by computing the derivative of the product of these two functions. This is easy enough to do directly.

[{left( {f,g} right)^prime } = {left( {{x^3}{x^6}} right)^prime } = {left( {{x^9}} right)^prime } = 9{x^8}]

Remember that on occasion we will drop the (left( x right)) part on the functions to simplify notation somewhat. We’ve done that in the work above.

Now, let’s try the following.

[f'left( x right)g'left( x right) = left( {3{x^2}} right)left( {6{x^5}} right) = 18{x^7}]

So, we can very quickly see that.

[{left( {f,g} right)^prime } ne f',g']

In other words, the derivative of a product is not the product of the derivatives.

Using the same functions we can do the same thing for quotients.

[{left( {frac{f}{g}} right)^prime } = {left( {frac{{{x^3}}}{{{x^6}}}} right)^prime } = {left( {frac{1}{{{x^3}}}} right)^prime } = {left( {{x^{ - 3}}} right)^prime } = - 3{x^{ - 4}} = - frac{3}{{{x^4}}}] [frac{{f'left( x right)}}{{g'left( x right)}} = frac{{3{x^2}}}{{6{x^5}}} = frac{1}{{2{x^3}}}]

So, again we can see that,

[{left( {frac{f}{g}} right)^prime } ne frac{{f'}}{{g'}}]

To differentiate products and quotients we have the Product Rule and the Quotient Rule.

Product Rule

If the two functions (fleft( x right)) and (gleft( x right)) are differentiable (i.e. the derivative exist) then the product is differentiable and,

[{left( {f,g} right)^prime } = f',g + f,g']

The proof of the Product Rule is shown in the Proof of Various Derivative Formulas section of the Extras chapter.

Quotient Rule

If the two functions (fleft( x right)) and (gleft( x right)) are differentiable (i.e. the derivative exist) then the quotient is differentiable and,

[{left( {frac{f}{g}} right)^prime } = frac{{f',g - f,g'}}{{{g^2}}}]

Note that the numerator of the quotient rule is very similar to the product rule so be careful to not mix the two up!

The proof of the Quotient Rule is shown in the Proof of Various Derivative Formulas section of the Extras chapter.

Let’s do a couple of examples of the product rule.

Example 1 Differentiate each of the following functions.

1. (y = sqrt[3]{{{x^2}}}left( {2x - {x^2}} right))
2. (fleft( x right) = left( {6{x^3} - x} right)left( {10 - 20x} right))

Show All SolutionsHide All Solutions

3.1 Product Ruleap Calculus Calculator

At this point there really aren’t a lot of reasons to use the product rule. As we noted in the previous section all we would need to do for either of these is to just multiply out the product and then differentiate.

With that said we will use the product rule on these so we can see an example or two. As we add more functions to our repertoire and as the functions become more complicated the product rule will become more useful and in many cases required.

a (y = sqrt[3]{{{x^2}}}left( {2x - {x^2}} right)) Show Solution

Note that we took the derivative of this function in the previous section and didn’t use the product rule at that point. We should however get the same result here as we did then.

Now let’s do the problem here. There’s not really a lot to do here other than use the product rule. However, before doing that we should convert the radical to a fractional exponent as always.

[y = {x^{frac{2}{3}}}left( {2x - {x^2}} right)]

Now let’s take the derivative. So, we take the derivative of the first function times the second then add on to that the first function times the derivative of the second function.

[y' = frac{2}{3}{x^{ - frac{1}{3}}}left( {2x - {x^2}} right) + {x^{frac{2}{3}}}left( {2 - 2x} right)]

This is NOT what we got in the previous section for this derivative. However, with some simplification we can arrive at the same answer.

[y' = frac{4}{3}{x^{frac{2}{3}}} - frac{2}{3}{x^{frac{5}{3}}} + 2{x^{frac{2}{3}}} - 2{x^{frac{5}{3}}} = frac{{10}}{3}{x^{frac{2}{3}}} - frac{8}{3}{x^{frac{5}{3}}}]

This is what we got for an answer in the previous section so that is a good check of the product rule.

b (fleft( x right) = left( {6{x^3} - x} right)left( {10 - 20x} right)) Show Solution

This one is actually easier than the previous one. Let’s just run it through the product rule.

[begin{align*}f'left( x right) & = left( {18{x^2} - 1} right)left( {10 - 20x} right) + left( {6{x^3} - x} right)left( { - 20} right) & = - 480{x^3} + 180{x^2} + 40x - 10end{align*}]

Since it was easy to do we went ahead and simplified the results a little.

Let’s now work an example or two with the quotient rule. In this case, unlike the product rule examples, a couple of these functions will require the quotient rule in order to get the derivative. The last two however, we can avoid the quotient rule if we’d like to as we’ll see.

Example 2 Differentiate each of the following functions.

1. (displaystyle Wleft( z right) = frac{{3z + 9}}{{2 - z}})
2. (displaystyle hleft( x right) = frac{{4sqrt x }}{{{x^2} - 2}})
3. (displaystyle fleft( x right) = frac{4}{{{x^6}}})
4. (displaystyle y = frac{{{w^6}}}{5})

3.1 Product Ruleap Calculus Solver

Show All SolutionsHide All Solutionsa (displaystyle Wleft( z right) = frac{{3z + 9}}{{2 - z}}) Show Solution

There isn’t a lot to do here other than to use the quotient rule. Here is the work for this function.

[begin{align*}W'left( z right) & = frac{{3left( {2 - z} right) - left( {3z + 9} right)left( { - 1} right)}}{{{{left( {2 - z} right)}^2}}} & = frac{{15}}{{{{left( {2 - z} right)}^2}}}end{align*}]
b

3.1 Product Ruleap Calculus Formulas

(displaystyle hleft( x right) = frac{{4sqrt x }}{{{x^2} - 2}}) Show Solution

Again, not much to do here other than use the quotient rule. Don’t forget to convert the square root into a fractional exponent.

[begin{align*}h'left( x right) & = frac{{4left( {{textstyle{1 over 2}}} right){x^{ - frac{1}{2}}}left( {{x^2} - 2} right) - 4{x^{frac{1}{2}}}left( {2x} right)}}{{{{left( {{x^2} - 2} right)}^2}}} & = frac{{2{x^{frac{3}{2}}} - 4{x^{ - frac{1}{2}}} - 8{x^{frac{3}{2}}}}}{{{{left( {{x^2} - 2} right)}^2}}} & = frac{{ - 6{x^{frac{3}{2}}} - 4{x^{ - frac{1}{2}}}}}{{{{left( {{x^2} - 2} right)}^2}}}end{align*}]
c (displaystyle fleft( x right) = frac{4}{{{x^6}}}) Show Solution

It seems strange to have this one here rather than being the first part of this example given that it definitely appears to be easier than any of the previous two. In fact, it is easier. There is a point to doing it here rather than first. In this case there are two ways to do compute this derivative. There is an easy way and a hard way and in this case the hard way is the quotient rule. That’s the point of this example.

Let’s do the quotient rule and see what we get.

[f'left( x right) = frac{{left( 0 right)left( {{x^6}} right) - 4left( {6{x^5}} right)}}{{{{left( {{x^6}} right)}^2}}} = frac{{ - 24{x^5}}}{{{x^{12}}}} = - frac{{24}}{{{x^7}}}]

Now, that was the “hard” way. So, what was so hard about it? Well actually it wasn’t that hard, there is just an easier way to do it that’s all. However, having said that, a common mistake here is to do the derivative of the numerator (a constant) incorrectly. For some reason many people will give the derivative of the numerator in these kinds of problems as a 1 instead of 0! Also, there is some simplification that needs to be done in these kinds of problems if you do the quotient rule.

The easy way is to do what we did in the previous section.

[fleft( x right) = 4{x^{ - 6}} hspace{0.5in} f'left( x right) = - 24{x^{ - 7}} = - frac{{24}}{{{x^7}}}]

Either way will work, but I’d rather take the easier route if I had the choice.

d (displaystyle y = frac{{{w^6}}}{5}) Show Solution

This problem also seems a little out of place. However, it is here again to make a point. Do not confuse this with a quotient rule problem. While you can do the quotient rule on this function there is no reason to use the quotient rule on this. Simply rewrite the function as

[y = frac{1}{5}{w^6}]

and differentiate as always.

[y' = frac{6}{5}{w^5}]

Finally, let’s not forget about our applications of derivatives.

3.1 Product Ruleap Calculus 14th Edition

Example 3 Suppose that the amount of air in a balloon at any time (t) is given by [Vleft( t right) = frac{{6sqrt[3]{t}}}{{4t + 1}}]

Determine if the balloon is being filled with air or being drained of air at (t = 8).

Show Solution

If the balloon is being filled with air then the volume is increasing and if it’s being drained of air then the volume will be decreasing. In other words, we need to get the derivative so that we can determine the rate of change of the volume at (t = 8).

This will require the quotient rule.

[begin{align*} {V}'left( t right) & =frac{2{{t}^{-frac{2}{3}}}left( 4t+1 right)-6{{t}^{frac{1}{3}}}left( 4 right)}{{{left( 4t+1 right)}^{2}}} & =frac{-16{{t}^{frac{1}{3}}}+2{{t}^{-frac{2}{3}}}}{{{left( 4t+1 right)}^{2}}} & =frac{-16{{t}^{frac{1}{3}}}+{}^{2}/{}_{{{t}^{tfrac{2}{3}}}}}{{{left( 4t+1 right)}^{2}}} end{align*}]

Note that we simplified the numerator more than usual here. This was only done to make the derivative easier to evaluate.

The rate of change of the volume at (t = 8) is then,

[begin{align*}V'left( 8 right) & = frac{{ - 16left( 2 right) + frac{2}{4}}}{{{{left( {33} right)}^2}}}hspace{0.25in}hspace{0.25in}{left( 8 right)^{frac{1}{3}}} = 2hspace{0.25in}{left( 8 right)^{frac{2}{3}}} = {left( {{{left( 8 right)}^{frac{1}{3}}}} right)^2} = {left( 2 right)^2} = 4 & = - frac{{63}}{{2178}} = - frac{7}{{242}}end{align*}]

So, the rate of change of the volume at (t = 8) is negative and so the volume must be decreasing. Therefore, air is being drained out of the balloon at (t = 8).

As a final topic let’s note that the product rule can be extended to more than two functions, for instance.

[begin{align*}{left( {f,g,h} right)^prime } & = f',g,h + f,g',h + f,g,h' & {left( {f,g,h,w} right)^prime } = f',g,h,w + f,g',h,w + f,g,h',w + f,g,h,w'end{align*}]

Deriving these products of more than two functions is actually pretty simple. For example, let’s take a look at the three function product rule.

First, we don’t think of it as a product of three functions but instead of the product rule of the two functions (f,g) and (h) which we can then use the two function product rule on. Doing this gives,

[{left( {f,g,h} right)^prime } = {left( {left[ {f,g} right],h} right)^prime } = {left[ {f,g} right]^prime }h + left[ {f,g} right]h']

Note that we put brackets on the (f,g) part to make it clear we are thinking of that term as a single function. Now all we need to do is use the two function product rule on the ({left[ {f,g} right]^prime }) term and then do a little simplification.

[{left( {f,g,h} right)^prime } = left[ {f',g + f,g'} right]h + left[ {f,g} right]h' = f',g,h + f,g',h + f,g,h']

Any product rule with more functions can be derived in a similar fashion.

With this section and the previous section we are now able to differentiate powers of (x) as well as sums, differences, products and quotients of these kinds of functions. However, there are many more functions out there in the world that are not in this form. The next few sections give many of these functions as well as give their derivatives.

We start with the derivative of a power function, $ds f(x)=x^n$. Here $n$ is a number of any kind: integer,rational, positive, negative, even irrational, as in $ds x^pi$. We havealready computed some simple examples, so the formula should not be acomplete surprise:$${dover dx}x^n = nx^{n-1}.$$It is not easy to show this is true for any $n$. We will do some ofthe easier cases now, and discuss the rest later.

The easiest, and most common, is the case that $n$ is a positiveinteger. To compute the derivative we need to compute the followinglimit:$${dover dx}x^n = lim_{Delta xto0} {(x+Delta x)^n-x^nover Delta x}.$$For a specific, fairly small value of $n$, we could do this bystraightforward algebra.

Example 3.1.1 Find the derivative of $ds f(x)=x^3$.$$eqalign{{dover dx}x^3 &= lim_{Delta xto0} {(x+Delta x)^3-x^3over Delta x}.cr&=lim_{Delta xto0} {x^3+3x^2Delta x+3xDelta x^2 + Delta x^3-x^3over Delta x}.cr&=lim_{Delta xto0}{3x^2Delta x+3xDelta x^2 + Delta x^3over Delta x}.cr&=lim_{Delta xto0}3x^2+3xDelta x + Delta x^2 = 3x^2.cr}$$

The general case is really not much harder as long as we don't try todo too much. The key is understanding what happens when $ds (x+Delta x)^n$is multiplied out:$$(x+Delta x)^n=x^n + nx^{n-1}Delta x + a_2x^{n-2}Delta x^2+cdots++a_{n-1}xDelta x^{n-1} + Delta x^n.$$We know that multiplying out will give a large number of terms all ofthe form $ds x^iDelta x^j$, and in fact that $i+j=n$ in every term. Oneway to see this is to understand that one method for multiplying out $ds (x+Delta x)^n$ is the following: In every $(x+Delta x)$ factor,pick either the $x$ or the $Delta x$, then multiply the $n$ choicestogether; do this in all possible ways. For example, for $ds (x+Delta x)^3$, there are eight possible ways to do this:$$eqalign{(x+Delta x)(x+Delta x)(x+Delta x)&=xxx + xxDelta x + xDelta x x+ xDelta x Delta xcr&qquad+ Delta x xx + Delta xxDelta x + Delta xDelta x x+ Delta xDelta x Delta xcr&= x^3 + x^2Delta x +x^2Delta x +xDelta x^2cr&quad+x^2Delta x +xDelta x^2 +xDelta x^2 +Delta x^3cr&=x^3 + 3x^2Delta x + 3xDelta x^2+Delta x^3cr}$$No matter what $n$ is, there are $n$ ways to pick $Delta x$ in onefactor and $x$ in the remaining $n-1$ factors; this means one term is$ds nx^{n-1}Delta x$. The other coefficients are somewhat harder tounderstand, but we don't really need them, so in the formula abovethey have simply been called $ds a_2$, $ds a_3$, and so on. We know that everyone of these terms contains $Delta x$ to at least the power 2. Nowlet's look at the limit:$$eqalign{{dover dx}x^n &= lim_{Delta xto0} {(x+Delta x)^n-x^nover Delta x}cr&=lim_{Delta xto0} {x^n + nx^{n-1}Delta x + a_2x^{n-2}Delta x^2+cdots+a_{n-1}xDelta x^{n-1} + Delta x^n-x^nover Delta x}cr&=lim_{Delta xto0} {nx^{n-1}Delta x + a_2x^{n-2}Delta x^2+cdots+a_{n-1}xDelta x^{n-1} + Delta x^nover Delta x}cr&=lim_{Delta xto0} nx^{n-1} + a_2x^{n-2}Delta x+cdots+a_{n-1}xDelta x^{n-2} + Delta x^{n-1} = nx^{n-1}.cr}$$

Now without much trouble we can verify the formula for negativeintegers. First let's look at an example:

Example 3.1.2 Find the derivative of $ds y=x^{-3}$. Using the formula,$ds y'=-3x^{-3-1}=-3x^{-4}$.

Here is the general computation. Suppose $n$ is a negative integer;the algebra is easier to follow if we use $n=-m$ in the computation,where $m$ is a positive integer.$$eqalign{{dover dx}x^n &= {dover dx}x^{-m} =lim_{Delta xto0} {(x+Delta x)^{-m}-x^{-m}over Delta x}cr&=lim_{Delta xto0} { {1over (x+Delta x)^m} - {1over x^m} over Delta x} cr&=lim_{Delta xto0} { x^m - (x+Delta x)^m over(x+Delta x)^m x^m Delta x} cr&=lim_{Delta xto0} { x^m - (x^m + mx^{m-1}Delta x + a_2x^{m-2}Delta x^2+cdots+a_{m-1}xDelta x^{m-1} + Delta x^m)over(x+Delta x)^m x^m Delta x} cr&=lim_{Delta xto0} { -mx^{m-1} - a_2x^{m-2}Delta x-cdots-a_{m-1}xDelta x^{m-2} - Delta x^{m-1})over(x+Delta x)^m x^m} cr&={ -mx^{m-1} over x^mx^m}={ -mx^{m-1} over x^{2m}}=-mx^{m-1-2m}= nx^{-m-1} = nx^{n-1}.cr}$$

We will later see why the other cases of the power rule work, but fromnow on we will use the power rule whenever $n$ is any real number.Let's note here a simple case in which the power rule applies, oralmost applies, but is not really needed. Suppose that $f(x)=1$;remember that this '1' is a function, not 'merely' a number, andthat $f(x)=1$ has a graph that is a horizontal line, with slope zeroeverywhere. So we know that $f'(x)=0$. We might also write $ds f(x)=x^0$,though there is some question about just what this means at $x=0$. Ifwe apply the power rule, we get $ds f'(x)=0x^{-1}=0/x=0$, again notingthat there is a problem at $x=0$. So the power rule 'works' in thiscase, but it's really best to just remember that the derivative of anyconstant function is zero.

Exercises 3.1

Find the derivatives of the given functions.

Ex 3.1.1$ds x^{100}$(answer)

Ex 3.1.2$ds x^{-100}$(answer)

Ex 3.1.3$displaystyle {1over x^5}$(answer)

Ex 3.1.4$ds x^pi$(answer)

Ex 3.1.5$ds x^{3/4}$(answer)

Ex 3.1.6$ds x^{-9/7}$(answer)